目录

• 机器学习第一周笔记
  • 概述
    • 什么是机器学习？
    • 机器学习的分类
  • 线性回归
    • 回归模型
    • 梯度下降(Gradient descent)

机器学习第一周笔记

概述

什么是机器学习？

从字面上来说，机器学习就是让机器通过模仿人学习的过程学习。也就是说让机器有能力学习，而不是通过准确的程序而实现。我们生活中无处不在存在着机器学习的应用，例如垃圾邮件分类系统，通过图片识别物体等。

机器学习的分类

机器学习分为两大类：

目录

• 反引号`
• repr函数
• 关于单例的思考

反引号`

今天在看一本基于python2.2的Design Pattern书，其中有一段关于单例的代码我很不解，因为用到了反引号`，也就是reverse quotes。书中代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class OnlyOne:
  class __OnlyOne:
    def __init__(self, arg):
      self.val = arg
    def __str__(self):
      return `self` + self.val
  instance = None
  def __init__(self, arg):
    if not OnlyOne.instance:
      OnlyOne.instance = OnlyOne.__OnlyOne(arg)
    else:
      OnlyOne.instance.val = arg
  def __getattr__(self, name):
    return getattr(self.instance, name)

x = OnlyOne('sausage')
print x
y = OnlyOne('eggs')
print y
z = OnlyOne('spam')
print z
print x
print y
print `x`
print `y`
print `z`

目录

• 可迭代对象
• 迭代器
• 生成器
• 关键词Yield
• 什么时候使用生成器
• 从Design Pattern角度看生成器

可迭代对象

要想理解python中的生成器，得先从可迭代对象Iterable说起。什么是可迭代对象呢？

定义了可以返回一个迭代器的__iter__方法的对象，或者定义了可以支持下标索引的__getitem__方法的对象，就是一个可迭代对象

所以我们可以用如下方法来判断一个实例是否为可迭代对象

1
2
3
4
5
6
7
8

hasattr((1,2,3), '__iter__') # True

hasattr([1,2,3], '__iter__') # True

hasattr({}, '__iter__') # True

hasattr('abc', '__getitem__') # True

知道了可迭代对象的定义，那么可迭代对象又有什么用呢，如下列所示，我们经常在python中使用for…in循环，那么for…in循环能在所有对象上使用吗？

最近在看一本基于pyhton的Design Pattern方面的书，其中涉及到了python的多态，也就是polymorphism。用python来解释，到底什么是多态(polymorphism)呢？StackOverflow上有一个很好的答案，下面便是答案中举的例子

目录

• 制作Ubuntu启动U盘
• 安装Ubuntu
• 解决驱动问题
  • 安装killer网卡驱动
  • 安装蓝牙驱动
• 进阶配置AlienFx

作为一个游戏发烧友，同时也是小白全栈开发程序员我买了Alienware却只用来打游戏是在是太可惜了。为了搞搞开发，昨天配置了一天WSL (Windows Subsystems for Linxu)，用了Hyper+zsh的终端组合。其中在zsh中输入atom能启动windows的Atom也着实把我惊艳了一把，但其实也就算仅限于打开而已。事实是Windows中的文本编辑器并不能直接编辑其子系统中的文件。所以这个子系统在某些方便我觉得还没有Vagrant方便，没有图形界面，意味着不能使用Atom，Visual Studio Code这样代表先进生产力的工具，于是配置WSL搞搞开发的想法就此作罢。

子系统搞不成，于是有了直接在Ubuntu上工作的想法。其实Alienware上安装Ubuntu不是很难，除了一些蓝牙和Wi-Fi方面的兼容问题，安装过程非常顺利。接下来step by step记录安装过程。

目录

• 安装IBus中文输入法
• 安装搜狗中文输入法

安装IBus中文输入法

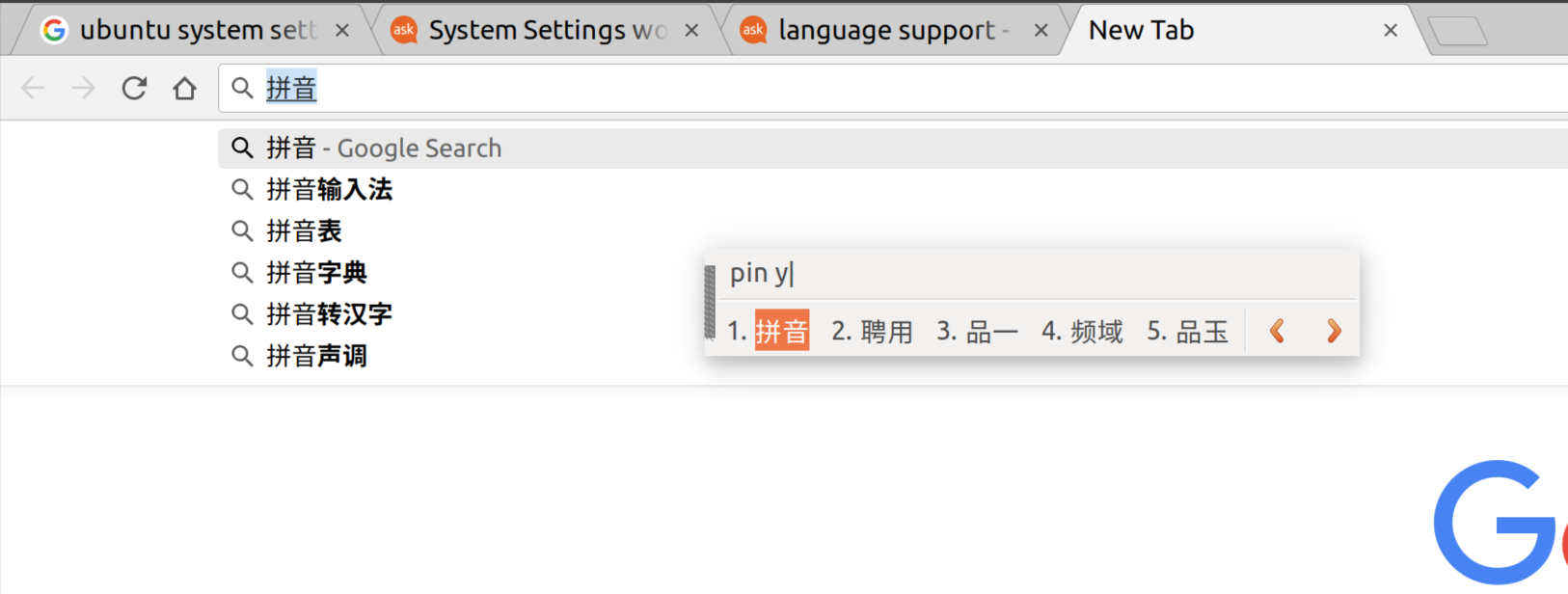
最近又重新安装了Ubuntu系统。因为要写中文博客，没有中文输入法实在是麻烦。在Ubuntu上安装中文输入法确实没有Windows上显而易见，所以写下步骤方便自己将来参考。

1. 首先进入系统设置选择language support，如果没有完整安装该功能，先根据系统提示完成安装

2. 点击install/remove language 来安装中文支持

3. 接下来在Terminal中手动安装下面任何一个输入法

   sudo apt-get install ibus-pinyin

   sudo apt-get install ibus-sunpinyin

4. 重启IBus daemon

   ibus restart

5. 再进入系统设置选择Text Entry，点击左下角的小加号并在add input source界面中搜索Chinese，选择一款拼音输入法

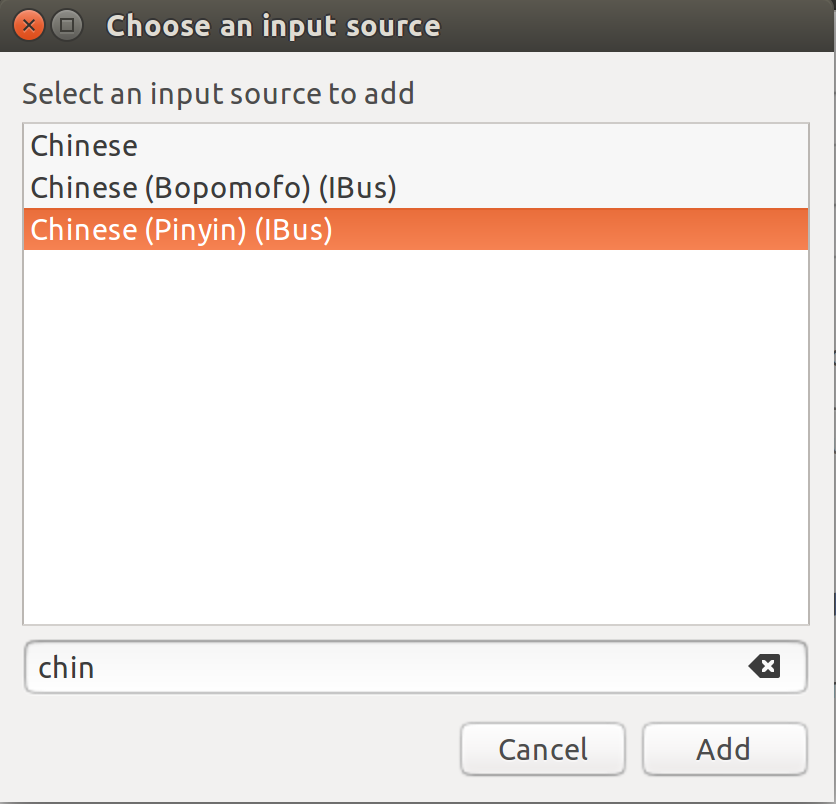
6. 使用吧

安装搜狗中文输入法

使用了几天IBus的中文输入发，使用体验简直弱爆了。首先4k屏适配有问题，待选框时刻游离在屏幕之外，然而最致命的是，IBus拼音输入法竟然有切换到双拼就无法再切换回来的bug。早年间我在ubuntu 14上使用过搜狗输入法，用户体验良好，于是试着在ubuntu 16.04上安装。虽然安装步骤比在ubuntu 14上稍稍复杂一些，但是搜狗输入法完美适配4k屏幕而且一如既往的好用。安装步骤如下：

算法复杂度分析

设输入数组长度为N，最优情况在输入数组的最大值不等于N时达成

算法分析

permutation 被定义为长为N的数组，包含整数1到N，且每个整数包含有且仅有一次。根据定义，我们必须遍历完输入数组才能知道是否1到N的每个整数包含有且仅有一次，所以算法复杂度为O(N)且无法继续优化。如何检测输入数组中1到N的每个整数出现有且仅有一次呢？一个比较直观的方法是用一个长度为N的数组作标记，遍历输入数组并在标记数组的对应项作标记，一旦该标记数组所有项均被标记，则说明输入数组满足permutation定义。但是该方法有一个缺点，就是需要成比例于输入数组长度N的存储空间。有没有不需要额外存储空间的算法呢？答案当然是有的，技巧在于利用输入数组，在遍历输入数组的同时，利用输入数组做标记。由于输入数组各项均为正整数，我们可以将某一项置为负值来标记该项索引+1对应的正整数出现过一次。

源代码

1
2
3
4
5
6
7
8
9

def solution(A):
    # write your code in Python 2.7
    for i in xrange(len(A)):
        index = A[i] if A[i] > 0 else -A[i]
        if index > len(A) or A[index - 1] < 0:
            return 0
        else:
            A[index - 1] = -A[index - 1]
    return 1

算法复杂度分析

算法分析

创建检查数组check，遍历数组A的项，若某项的值为整数x，则以整数x作为索引，将check数组对应的项置1。在遍历check数组，寻找值为0时索引的最小值。

源代码

1
2
3
4
5
6
7
8
9
10
11
12

def solution(A):
    # write your code in Python 2.7
    n=len(A)
    max_A=100001
    check=[0]*(max_A+1)
    for i in xrange(n):
        if(A[i]>=0 and A[i]<max_A and check[A[i]-1]==0):
            check[A[i]-1]=1
    for ind in xrange(max_A+1):
        if(check[ind]==0):
            return ind+1
    return -1

算法复杂度分析

算法分析

若要达到最差情况下的时间复杂度为O(N+M)，那就意味着不能在A[K] = N + 1时依次将每个counter的值置为当前counters数组的最大值。因为max counter操作的复杂度为O(N)且需要嵌套在复杂度为O(M)的循环中，这样算法的复杂度至少为O(NM)。也就以为着当A[K] = N + 1时，我们不能立即执行max counter操作。借用下惰性求值的概念，只有在真的需要某个counter值的情况的下才执行计算。这就需要建立两个变量，max_A记录当前counters的最大值，lastUpdate记录上一次执行max counter操作时max_A的值。这样只有当A[K] = N + 1时，才把max_A的值赋值给lastUpdate。而当A[i] < N+1时，则要根据lastUpdate的值来更新counter和max_A的值。

最后在返回所counters数组值之前，需要根据lastUpdate的值对每个counter的值进行计算

源代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

def solution(N, A):
    # each element of array A is an integer within the range [1..N + 1]
    # N and M are integers within the range [1..100,000]
    M = len(A)
    max_A = 0
    lastUpdate = 0
    counters=[0]*N
    for i in xrange(M):
        if (A[i]==N+1):
            lastUpdate = max_A
        if (A[i]<N+1):
            if (counters[A[i]-1]<lastUpdate):
                counters[A[i]-1]=lastUpdate+1
                if (counters[A[i]-1]>max_A):
                    max_A=counters[A[i]-1]
            else:
                counters[A[i]-1]=counters[A[i]-1]+1
                if (counters[A[i]-1]>max_A):
                    max_A=counters[A[i]-1]
    for j in xrange(N):
        if (counters[j]<lastUpdate):
            counters[j]=lastUpdate
    return counters
#  time complexity: O(N + M)

算法复杂度分析

最优情况在输入数组长度小于河宽X下达成

算法分析

依次读取输入数组的项，当读取过的项的集合包含1到X在内的所有整数时，输出当前项的数组索引。对于记录读取过的项的集合，可以用一个长度为X+1的check数组来记录。若读取了整数z，就把整数z作为索引，将对应的项置1。对于判断读取过的项的集合是否包含1到X在内的所有整数，我们都可以遍历check数组，检查索引1到X对应的项是否全部为1，如果不是，则说明我们还没有包含1到X在内的所有整数。但是这样，该判断算法需要遍历check数组，复杂度为O(X)。不过有一个小技巧可以将该判断算法降为O(1)，那就是在check数组的基础上，再使用step_left变量来记录还需要读取多少个不同的整数后读取过的项的集合才能包含1到X在内的所有整数。若读取了整数z，除了把整数z作为索引，将对应的项置1外，还要根据条件来更新step_left的值。此时，检查算法只需要判断step_left是否为0即可得知读取过的项的集合是否包含1到X在内的所有整数了。

源代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14

def solution(X, A):
    # write your code in Python 2.7
    n = len(A)
    if (n < X):
        return -1
    step_left = X
    check = [0]*(X+1)
    for i in xrange(n):
        if (check[A[i]]==0):
            check[A[i]]=1
            step_left -=1
        if (step_left==0):
            return i
    return -1